Futoshiki
Calcudoku
![]()
Consecutive Sudoku
Oddpair Sudoku
Pro
Sudoku
![]()
Looking for puzzles for your book, magazine or newspaper?
|
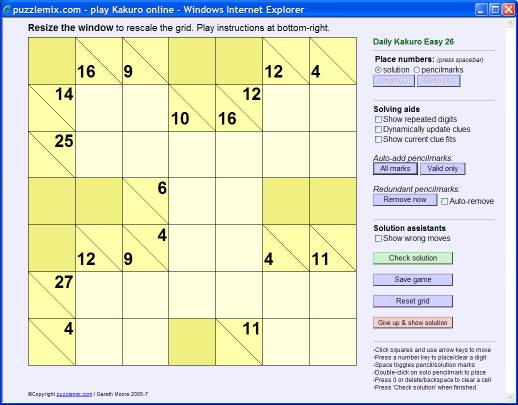
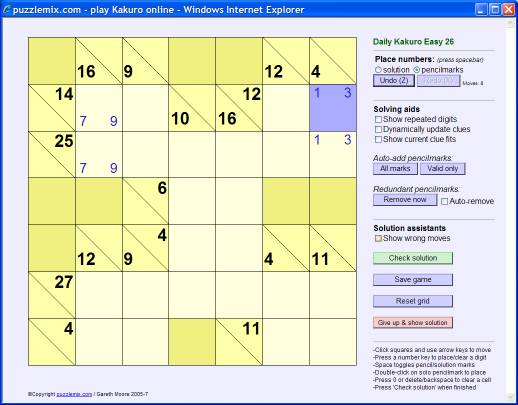
How to play Kakuro
The rules of Kakuro are simple - place the numbers 1 to 9 into the puzzle grid so that each continuous horizontal or vertical run of empty squares adds up to the value to the left of it or above it respectively. This value is shown either to the right or below a diagonal line. There is one other key rule: the same number cannot be repeated within any run, so the solution to the value '4' cannot be 2+2 but must 1+3 (or 3+1). You can repeat a number elsewhere in the same row or column so long as there is at least one clue or shaded square between them.
Look at the example puzzle above. There is only one possible solution for the '4' clue running down at the top-right. It must be 1+3 or 3+1, and this has been written in in 'pencilmarks' to note this. The same applies to the '16' clue at the top-left - the solution must be 7+9 or 9+7.
Now consider the '14' clue at the top-left. The solution to this cannot involve '7' because the answer would then be 7+7, which would repeat a number, so we can eliminate the 7 here as an option. The top-left square must contain 9, therefore, and so the square to its right must be 5 (9+5=14) and the square below must be 9. Similarly at the top-right, since we can only place 1 to 9 into the grid the top-right number cannot be '1' because the number to its left would need to be 11, which isn't allowed. So the top-right number must be 3, and then we can place the numbers next to it. Similar logic allows each corner of the puzzle to be completed:
By then progressing using logical reasoning (guessing is never needed) based on what numbers can fit into which square, the puzzle can be solved:
|