Futoshiki
Calcudoku
![]()
Consecutive Sudoku
Oddpair Sudoku
Pro
Sudoku
![]()
Looking for puzzles for your book, magazine or newspaper?
|
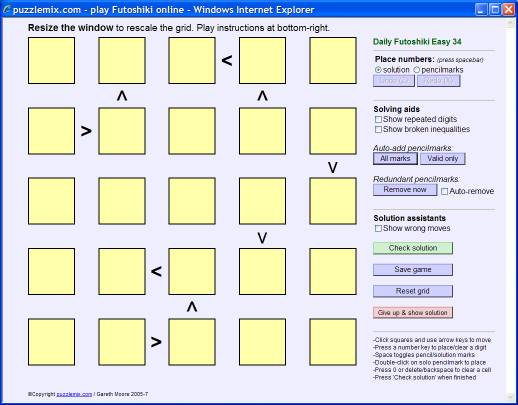
How to play Futoshiki
The aim of Futoshiki is to place the numbers 1 to 5 (or higher, if the puzzle is larger) into each row and column of the puzzle so that no number is repeated in a row or column and so that all of the inequality signs (< and >) are obeyed. This puzzle below is 5x5, so we must place 1 to 5 into it - if it was 6x6 we would need to place 1 to 6 into it, and so on.
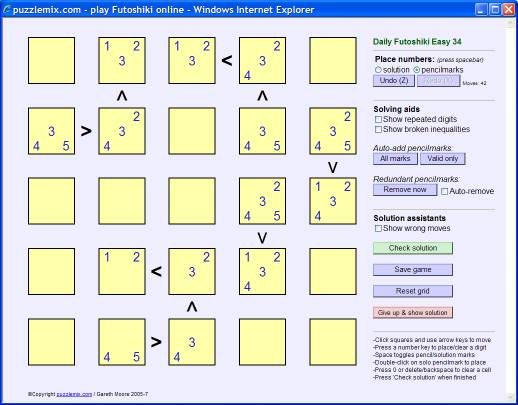
Look at the inequality signs. A less-than sign, <, means that the number it points at must be less than the number on the other side of the sign. Turned around the other way it becomes a greater-than sign, >, but the logic is still the same - the number it points at is smaller than the number on its other side. By paying attention to these inequality signs, we can eliminate some of the possibilities from the squares, as shown by the pencilmarks in the following grid:
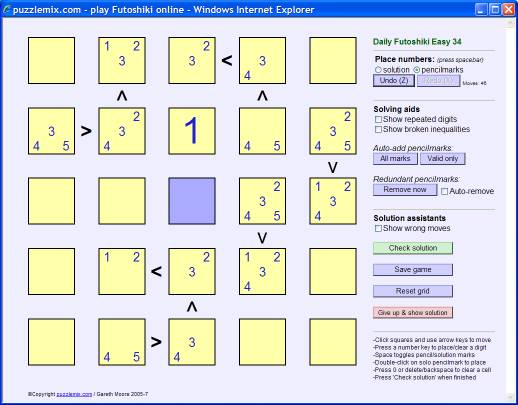
Look at the second row. By having made these eliminations we can see that the only place the '1' can go in this row is in the centre box. Once that is marked in we can eliminate '1' from some other squares, so updating the puzzle we now have the following possibilities:
Based on these deductions, the '5' must then go in the blue square in the centre column, the '4' in the same column must go in the bottom square, and so on. When the puzzle is fully-solved you will have 1 to 5 (or whatever the size of the puzzle is) in each row and column, and all of the inequality signs will be obeyed, as shown here:
|