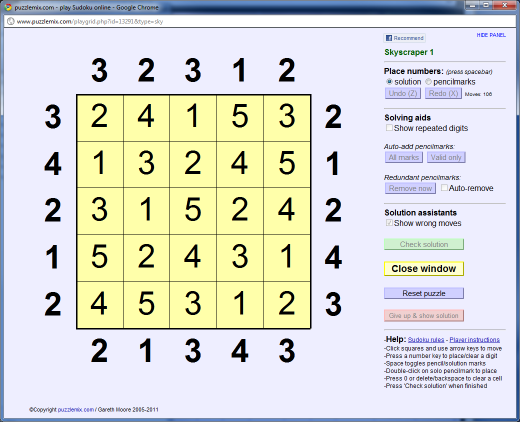
A Skyscraper puzzle consists of a square grid with some exterior 'skyscraper' clues. Every square in the grid must be filled with a digit from 1 to 5 (or 1 to whatever size the grid is) so that every row and column contains one of each digit, as in Sudoku or Futoshiki.
In Skyscraper each digit placed in the grid can be visualised as a building of that many storeys. A '5' is a 5 storey building, for example. Each number outside the grid reveals the number of 'buildings' that can be seen from that point, looking along the adjacent row or column. Every building blocks all buildings of a lower height from view, while taller buildings are still visible beyond it.
For example, if you look along a row and see "1 2 3 4 5" then the clue at the start of the row would be 5, since no building obscures any other. If instead you looked along and saw "1 3 4 5 2" then the clue would be 4, since 4 buildings can be seen (the 5 obscures the 2).
Try following the example below to clarify the rules. In this example the initial puzzle looks like this:
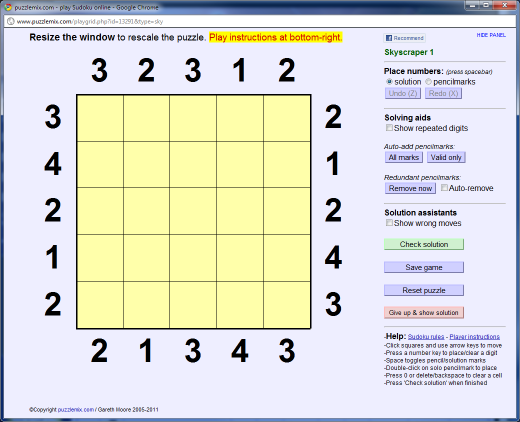
Look at the '1's around the edge. From these viewpoints only a single building can be seen, so it must be the tallest building. In this 5x5 puzzles you must place 1 to 5 in each row and column, so we can place the following four 5s:
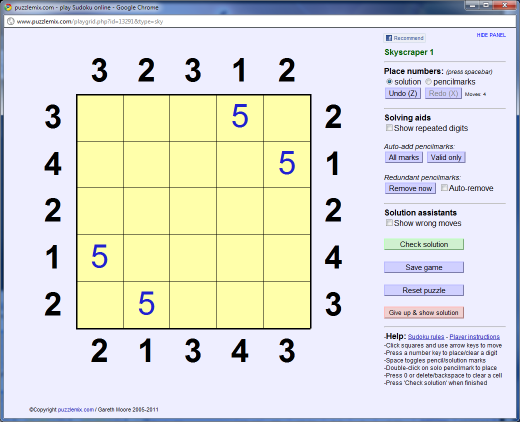
We can also place a 5 in the very centre of the grid, using regular Sudoku-esque rules (to ensure one of each digit in each row and column).
There are now various ways to progress from here. One option is to make use of the ability to add 'pencilmark' digits to the grid in order to keep track of which numbers can fit where. Using the '3' and '4' clues outside the grid we can be sure that there are no '4's in the outermost squares by these clues, and in the case of the '4' clue we know there aren't any '3's here either. We can mark in all candidates in these squares (also stepping another square into the row/column in the case of the '4' clues):
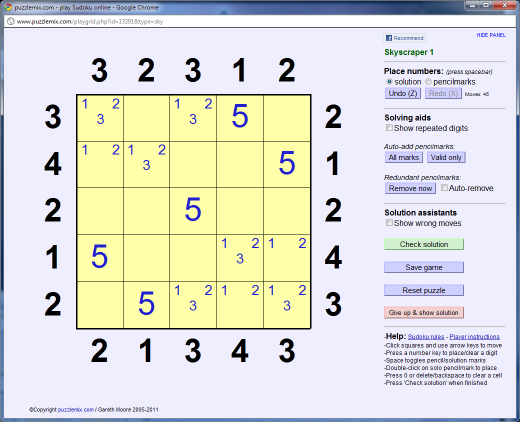
Noting our pencilmarks and looking at the bottom row we can see there is only place for the '4' to fit, so we can add this in.
We can also progress using the skyscraper logic more directly. Consider the '2' clue at the top of the second column. There must be a 4 at the very top of this column, otherwise 3 or more buildings would be visible.
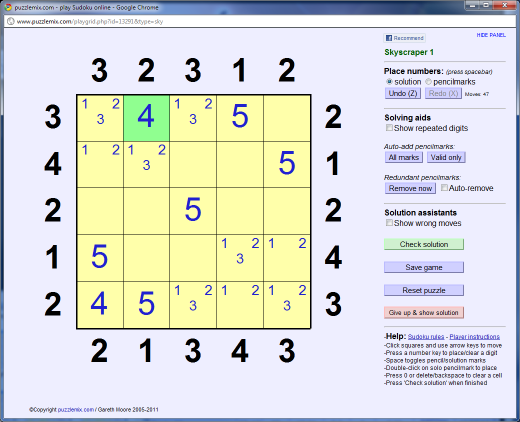
Similarly by elimination of other possible placements we can now place the '4' in the 4th row down, then the 4 in the 2nd row and finally the 4 in the 3rd row.
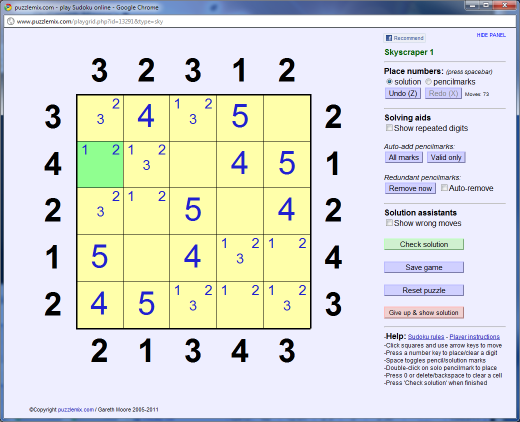
Look at the highlighted square above. The square beneath cannot contain a '1' because if it did then the '2' clue next to it would be wrong (we'd see 3 buildings from that point). So the highlighted square is the only place the '1' can fit in this column. If we add this we now have only one solution for this row that fulfils a '4' clue, since "1 2 3 4 5" would have given us a '5' clue. We can write this in.
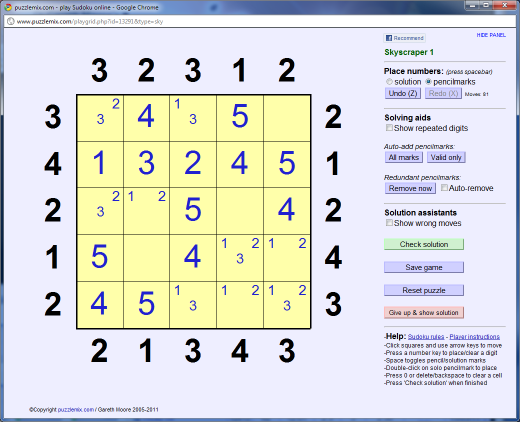
Similarly we can place the rest of the first column. It can't be "3 1 2 5 4" because that would have given a clue of '2', not '3', so it must be this:
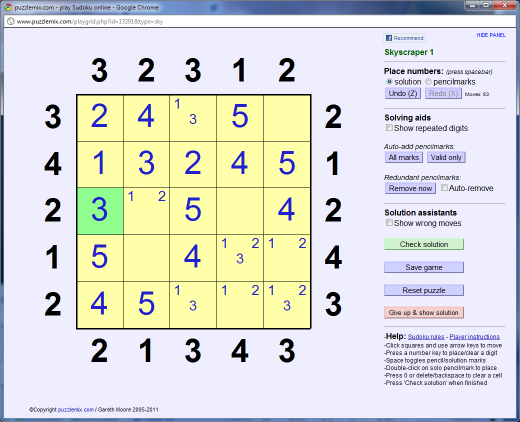
Now there is only one place for the '3' to fit on the 4th row:
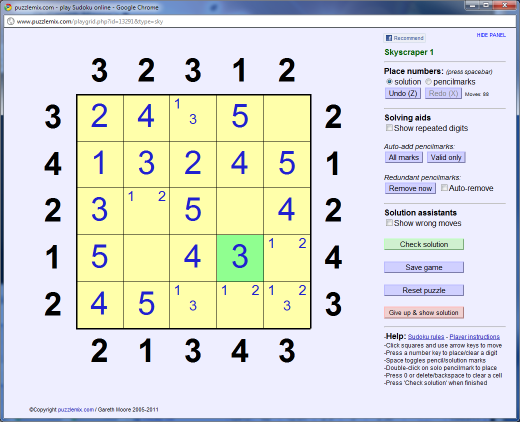
And finally we must have a '1', not a '3', at the top of the 3rd column to fulfil the '3' clue:
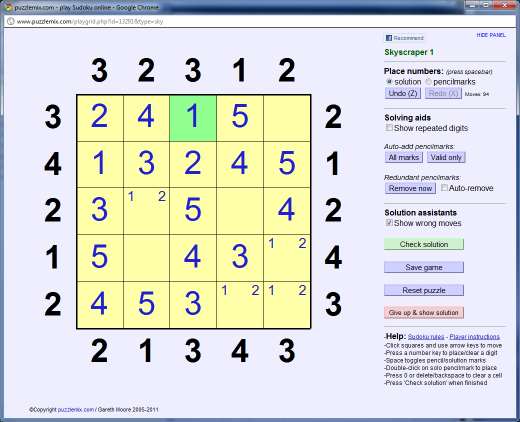
We can now follow through similarly to complete the grid: