Calcudoku combines the row and column constraints of Sudoku with numerical regions that are similar - but not identical - to those in Killer Sudoku.
To solve Calcudoku, place the numbers 1 to 6 (or whatever the width of the puzzle is) once each into every row and every column. Further, the given value at the top-left of each bold-lined region must be obtained when all of the numbers in that region have the given operation (+, -, ×, ÷) applied between them. For - and ÷ operations start with the largest number in the region and then subtract or divide by the other numbers.
In Mystery Calcudoku a '?' is given instead of an operation. In these you must work out the operation too - at least one of adding, subtracting, multiply or dividing results in the given total.
Note that there is no constraint on repeating numbers in bold-lined regions - calcudoku is different to jigsaw sudoku and killer sudoku puzzle in this respect.
To help understand the fundamental rules, consider the "1-" region at the top-left of the puzzle below. The two numbers in this region must result in 1 when the "-" operation is applied between them, with the smaller number subtracted from the larger. Therefore possible solutions to this region are 1 and 2 (since 2-1=1), or alternatively 2 and 3, or 3 and 4, or 4 and 5, or finally 5 and 6, and these could be written in either order into the two cells.

We can start solving this puzzle by writing in a few of the possible solutions to the numeric regions, beginning with some of those which have only one possible pair of digits. For example the "20×" in the top row can only be solved by 4 and 5 (4×5=20):
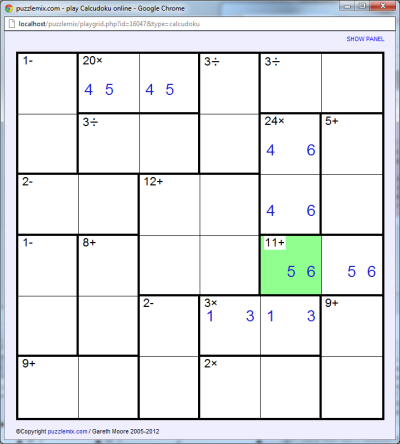
Note the cell in green. There must already be a 4 and 6 in this column, and since numbers cannot be repeated in a column we know this must be a 5. This also means there is only one solution to the 9+ region at the bottom-right now:
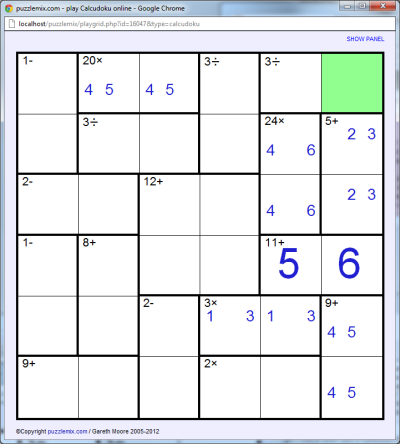
Because we must have each number from 1 to the size of the puzzle (6 in this case) in each row and column, we now know that the top-right-most cell in the grid must be a 1. This in turn lets us complete the 3÷ region that this 1 is now in with a 3, since 3÷1=3, and we also now can narrow the 2 and 6 in the top row down to two possible cells:
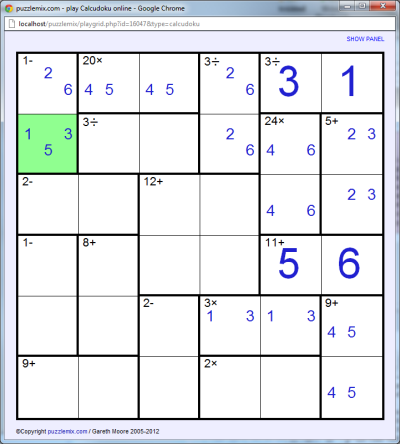
Notice how the green cell has three possible options to the two above it. This is because the possible solutions involving the 2 and 6 we have already placed are 6-5=1, 2-1=1 and 3-2=1 - i.e. the 1, 3 and 5 that are now options in that cell.
We can make several more deductions in a similar fashion, for example that the 2× in the bottom row must be solved by 1 and 2, and the elimination of the 3 from the right-most cell in the 3× region now that we have a 3 in that column already:
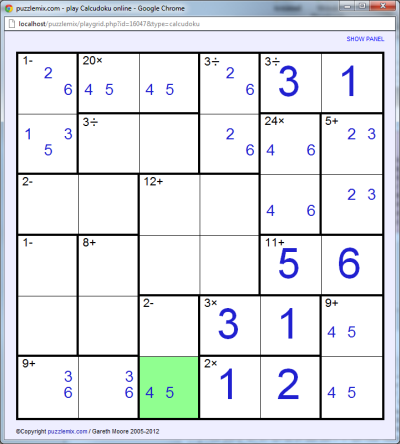
The cell marked in green is part of a 2- region. To use the 5 candidate the solution would need to be 5-3, but the 3 would share a row with an already-placed 3, so the solution must be 4. This in turn lets us complete more of the top row of the puzzle:
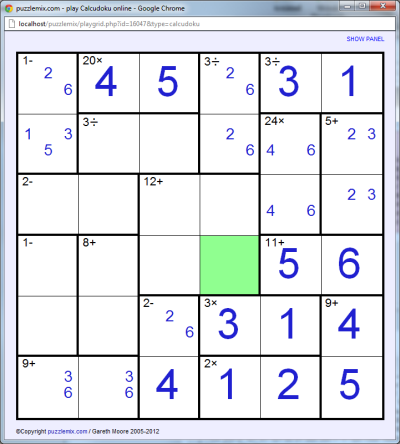
From here we need only make similar steps and soon we will have completed the entire puzzle:
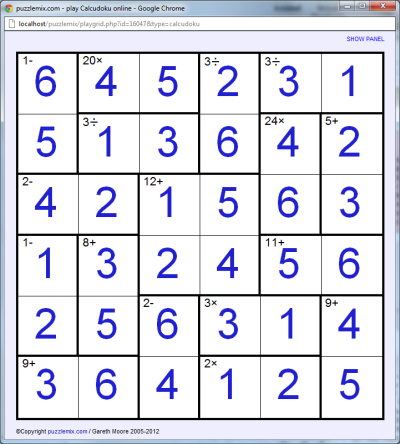
Calcudoku makes use of many of the same tricks that you will use on Sudoku and Killer Sudoku, but don't forget that numbers can repeat in bold-lined regions. This means, for example, that a 6+ region of 3 cells could be solved by 1, 1 and 4 (so long as the region was L-shaped, otherwise the row or column constraint would prevent the repeat).