Futoshiki
Calcudoku
![]()
Consecutive Sudoku
Oddpair Sudoku
Pro
Sudoku
![]()
Looking for puzzles for your book, magazine or newspaper?
|
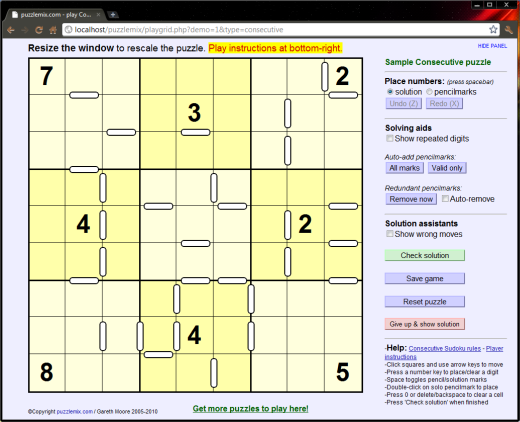
How to play Consecutive Sudoku
A Consecutive Sudoku puzzle adds one extra constraint to the standard Sudoku grid - not only must you place 1 to 9 (or 1 to whatever the width of the puzzle is) in each row, column and bold-lined box, but also obey the white consecutive markers:
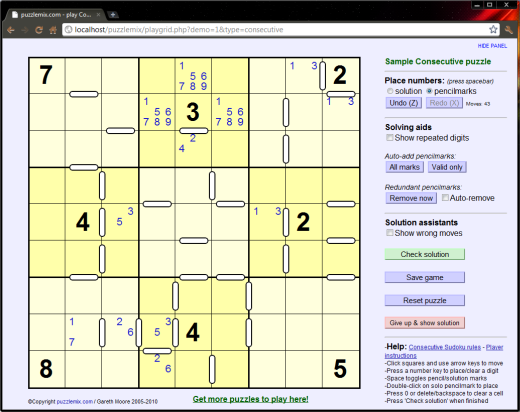
In the example puzzle shown here you can immediately narrow down the candidates next to some of the consecutive markers by comparing them with the pre-given numbers, as shown in the picture below. Small 'pencilmark' digits have been added to show valid values in these squares - pencilmarks are useful for helping keep track of possible solutions as you work through the puzzle. Because squares without markers between are not consecutive, you can also deduce further information, as I've marked in the top-middle of the 3x3 boxes as an example.
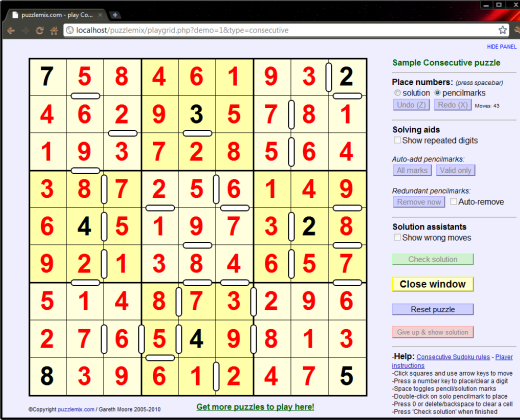
When this puzzle is fully-solved you will have 1 to 9 in each row, column and 3-by-3 box, and all numbers with white bars between will be consecutive and all numbers without white bars between will be non-consecutive as shown here:
And that's all there is to Consecutive Sudoku. |